背景
Aho–Corasick 算法(也称 AC 算法,AC 自动机)是由 Alfred V. Aho 和 Margaret J.Corasick 发明的字符串搜索算法,该算法在 1975 年产生于贝尔实验室,是著名的多模匹配算法之一。
一个典型应用就是:给出 k 个单词,再给出一段文章(长度是 n),让你找出有多少个单词在文章里出现过。
与其它模式串匹配不同,KMP 算法是单模式串的匹配算法,AC 算法是多模式串的匹配算法,匹配所需的时间复杂度是 O(n)。
AC 算法建立在字典树基础上,如果您还不了解字典树,可以参考字典树入门。
算法过程分析
以上述所说的典型应用为例,现给定 3 个单词 {“china”, “hit”, “use”},再给定一段文本 “chitchat”,求有多少个单词出现在文本中。
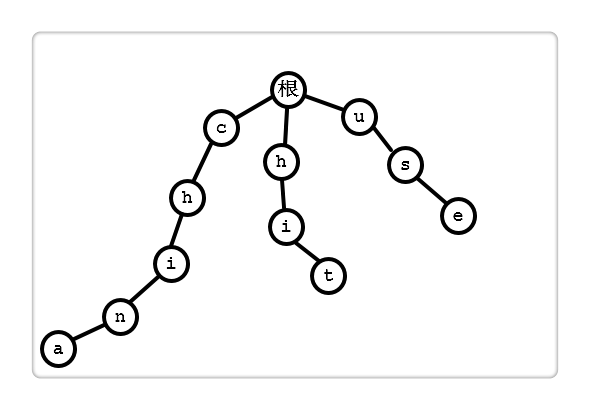
根据单词 {“china”, “hit”, “use”} 建立字典树。
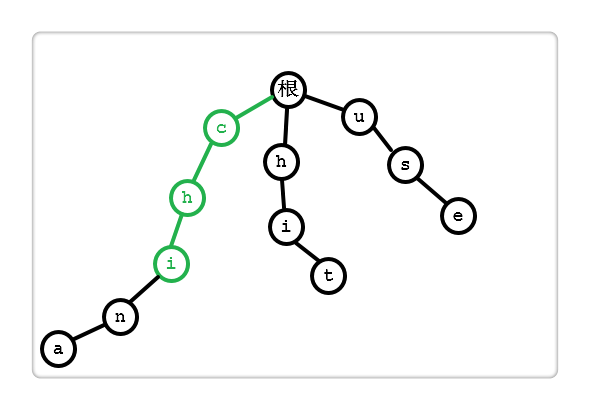
根据所给文本 “chitchat” 依次匹配,图中所示 “chi” 为匹配成功的字符串。
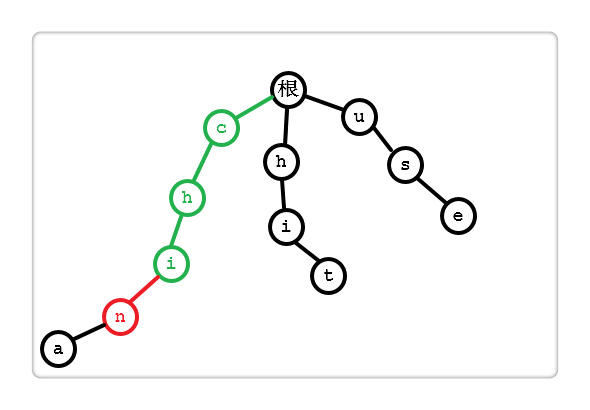
当匹配到第四个字符时,“t”和 “n” 匹配失败。
我们此时是知道已匹配成功的字符串的,即 “chi”。
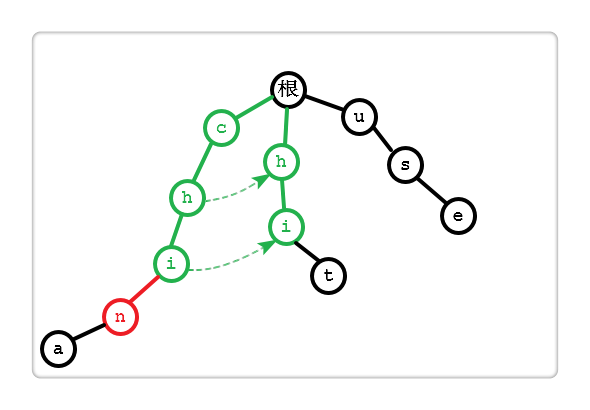
AC 算法的核心就是在所有给定的单词中,找到这样的一个单词,使其与已匹配成功字符串的相同前后缀最长,利用这个最长的相同前后缀实现搜索跳转。
如上图,单词 “hit” 与已匹配成功字符串 “chi” 的最长相同前后缀为 “hi”,因此下一步从单词“hit” 的“t”开始搜索。
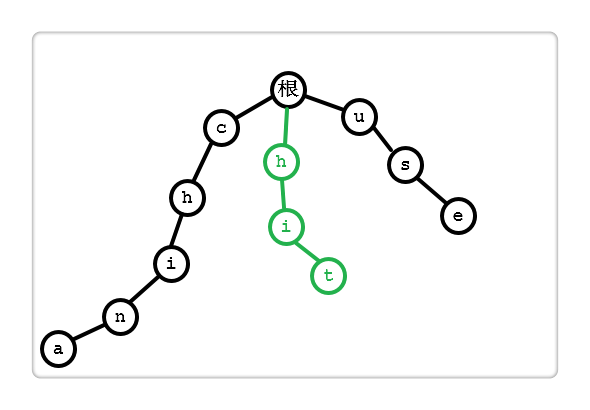
此时 “t” 是匹配的,在文本 “chitchat” 中找到一个单词“hit”。
其实到这里,AC 算法的思想已经基本呈现在大家面前了。剩下的问题就是如何解决第(3)步所述的 “核心”。
AC 算法核心
在每个结点里设置一个指针(我们称之为 fail 指针),指向跳转的位置。
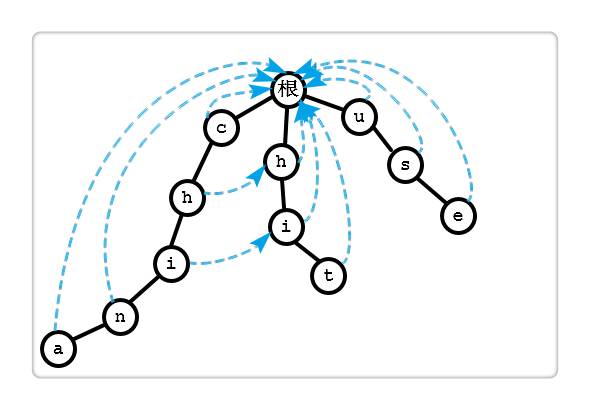
对于跳转位置的选择,基于以下两点:
对于根结点的所有儿子结点,它们的 fail 指针指向根结点;
而对于其它结点,不妨设该结点上的字符为ch,沿着它的父亲结点的 fail 指针走,直到走到一个结点,它的儿子中也有字符为ch的结点,然后把该结点的 fail 指针指向那个字符为ch的结点。如果一直走到了根结点都没找到,那就把 fail 指针指向根结点。
对于第 2 点,初学者可能有点不理解,我这里稍微解释下。请仔细阅读上面的第(3)步过程,利用父亲结点的最长相同前后缀来找到儿子的最长相同前后缀。
完整代码
/**
*
* author : 刘毅(Limer)
* date : 2017-08-10
* mode : C++
*/
#include <iostream>
#include <queue>
#define TREE_WIDTH 26
using namespace std;
struct Node
{
int end;
Node * fail;
Node * next[TREE_WIDTH];
Node()
{
this->end = 0;
this->fail = nullptr;
for (int i = 0; i < TREE_WIDTH; i++)
this->next[i] = nullptr;
}
};
class AC
{
private:
Node * root;
public:
AC();
~AC();
void destroy(Node * t);
void add(char * s);
void build_fail_pointer();
int ac_automaton(char * t);
};
AC::AC()
{
root = new Node;
}
AC::~AC()
{
destroy(root);
}
void AC::destroy(Node * t)
{
for (int i = 0; i < TREE_WIDTH; i++)
if (t->next[i])
destroy(t->next[i]);
delete t;
}
void AC::add(char * s)
{
Node * t = root;
while (*s)
{
if (t->next[*s – ‘a’] == nullptr)
t->next[*s – ‘a’] = new Node;
t = t->next[*s – ‘a’];
s++;
}
t->end++; // 假设单词可重复
}
void AC::build_fail_pointer()
{
queue<Node*> Q;
for (int i = 0; i < TREE_WIDTH; i++)
{
if (root->next[i])
{
Q.push(root->next[i]);
root->next[i]->fail = root;
}
}
Node * parent = nullptr;
Node * son = nullptr;
Node * p = nullptr;
while (!Q.empty())
{
parent = Q.front();
Q.pop();
for (int i = 0; i < TREE_WIDTH; i++)
{
if (parent->next[i])
{
Q.push(parent->next[i]);
son = parent->next[i];
p = parent->fail;
while (p)
{
if (p->next[i])
{
son->fail = p->next[i];
break;
}
p = p->fail;
}
if (!p) son->fail = root;
}
}
}
}
int AC::ac_automaton(char * t)
{
int ans = 0;
int pos;
Node * pre = root;
Node * cur = nullptr;
while (*t)
{
pos = *t – ‘a’;
if (pre->next[pos])
{
cur = pre->next[pos];
while (cur != root)
{
if (cur->end >= 0)
{
ans += cur->end;
cur->end = -1; // 避免重复查找
}
else
break; // 等于 -1 说明以前这条路径已找过,现在无需再找
cur = cur->fail;
}
pre = pre->next[pos];
t++;
}
else
{
if (pre == root)
t++;
else
pre = pre->fail;
}
}
return ans;
}
int main()
{
int n;
char s[1000];
while (1)
{
cout << “请输入单词个数:”;
cin >> n;
AC tree;
cout << “请输入” << n << “个单词:\n”;
while (n–)
{
cin >> s;
tree.add(s);
}
cout << “请输入搜索文本:”;
cin >> s;
tree.build_fail_pointer();
cout << “共有” << tree.ac_automaton(s) << “个单词匹配” << endl << endl;
}
return 0;
}
执行截图:

- 随机文章
标签云集
-
PHP小技巧
vue小技巧
adobe
树莓派
golang小技巧
nginx
linux
ios
前端开发
electron开发
前端技术
交互设计
iphone x
docker的使用
zabbix
数据库
logo
MySQL小知识
设计教程
php
图标设计
jupyter
docker
android
页面设计
python
k8s
Redis
Java
react
app设计
swoole
APP设计参考
css
ui设计
mysql优化
移动端识别
大数据可视化
webpack
分布式
docker命令
网页设计
JavaScript小技巧
python插件
APP UI设计
vue
javascript
mysql
设计灵感
docker小技巧



